The Logic of Pattern: Where Do They Come From?
Why have this discussion here?
This is a website with the principal purpose of sharing methods for drawing Islamic geometric Design. Most of the people who come to this site will follow the instructions without too much concern for where they came from. So long as the resulting pattern is correct and the layout methods are convenient, or at least not too painful, people will be satisfied. A substantial number of people who use my layouts do, however, ask where the layouts come from. This is the first part of the answer; this is a short, general overview of one possible logic of pattern.
All of the layouts found here are drawn by me.(1) What is presented here is one person’s point of view with a fairly consistent approach to pattern construction. If correct patterns with the desired symmetry result, any layout method is equally “valid.” The historical layout methods are unknown in any detail. My personal opinion is that some layout approaches contain more information, or teaching possibilities, regarding the underlying logic and structure of pattern. We may not be able to determine how the original craftsmen and artisans constructed pattern, line by line, but it is possible in many cases to see the broad shape of the thinking and the logic which went into creating the patterns. The genius of complex pattern design leaves traces to follow.
I think that it is worth writing out an outline of the logic I use since I find that it is different from many approaches. It may be wrong or irrelevant but it may have some merit as a prompt to your thinking about patterns. This short discussion will point out a large part of why I use the approach I do.
Question 1: What defines a Geometric Pattern?
For the designs studies here, from a part of the tradition of Islamic geometric design, we can limit this definition to “Repeating Patterns.” That just generates the question of; what repeats and how? The general answer is a very interesting discussion and was treated very well by Lewis Day in Pattern Design. (2) I think that the narrower answer for many Islamic geometric patterns gives a useful insight into how they are best approached.
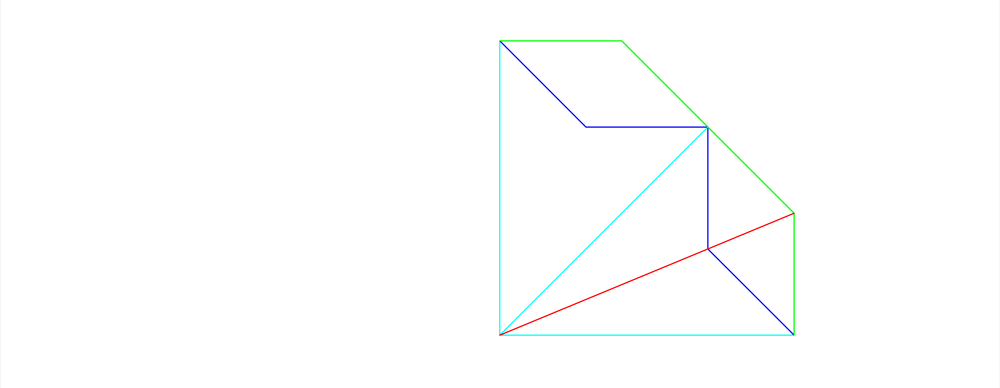
Consider this triangle
This triangle alone is not very exciting. How does it create a repeating pattern from the single dark blue line? I know two very important things about this triangle. The light blue and the green sides form a right angle and the dark blue lines is a bisector. I know one other thing about it but it will appear in a few moments.
How does this triangle create a pattern? There are a few ways. Triangles will tile a plane perfectly so we could just fill up the page with these, but it won’t be very interesting. What we want is to make the dark blue pattern line inside the triangle create a geometric pattern. To do that it needs to be continuous.
We do that by reflecting. The structure of the triangle is “reflected” across the red leg to give the result below. There are now two triangles that are mirror images of each other. We Already have everything we need for a classic Islamic geometric pattern but it isn’t very obvious yet.
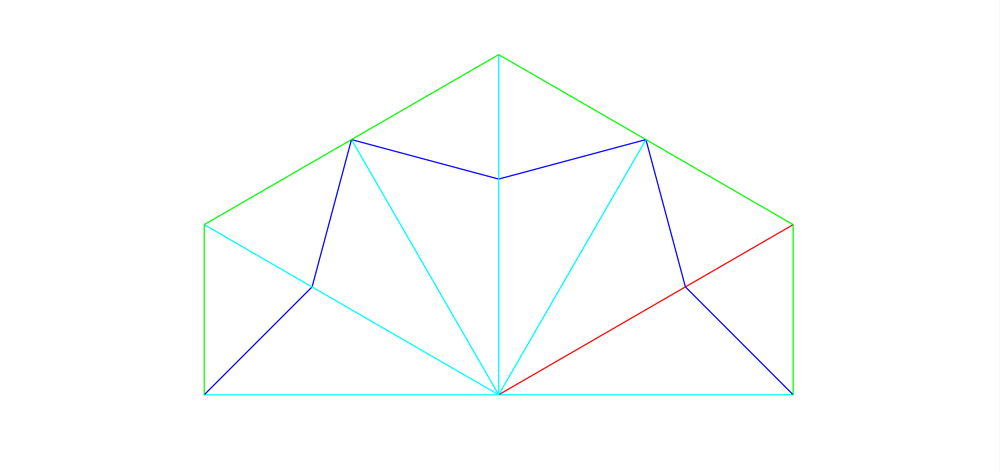
These two triangles, as a kite shape, can be reflected to give more pattern structure. This could also be viewed as reflecting just the original triangle two more times. A reflection of a reflection just puts you back where you started so that there will always be only two types of triangle building up the pattern.
If we keep going it rapidly becomes obvious where we are going.
This star polygon inside an octagon is just a simple triangle with a single line reflected around 15 times to meet itself, for 16 repeated triangles. We can call this entire construct a “Tile.” Tiles are the elements used to build Islamic geometric pattern. One or multiple tile types is used to completely cover the paper with pattern. There will be some references to tiling names and facts in these discussions but I will leave the vast majority of the terminology of tiling and symmetry groups as a separate investigation for those people who might be interested.
We can think of this as identical to the tile we would use on the kitchen walls or floor. Tiles are placed edge to edge to cover the space. There are a few rules about what we can put in the tile, but assembling them into patterns is simple to think about. Two of these tiles placed edge to edge develop the pattern, and show a problem. An octagon leaves gaps when it is tiled with itself.
Continuing the tiling gives a classic pattern which dates back far into the Roman empire. It is one of the first repeating geometric patterns incorporated into Islamic art. Several examples exist from Iraq in the 10th century CE.
This classic pattern was constructed from a simple triangle with one line inside it. It required one trivial operation repeated several times.
Why did that work?
The triangle was exactly one sixteenth of a full circle. This was the other crucial fact that I knew about the triangle. It was an integer “division” of the circle.
Question 2: Is This General?
That’s nice but it’s only an amusing story unless it is more general. Consider the triangle below.
Much of the structure of this triangle is the same as the first. The angle which will be at the center of the finished tile has changed; this will not be the same division of the circle.
Performing the same operations of reflection create a new tile.
We obviously started with a one twelfth division of the circle. Reflecting the triangle until the circle closes creates another tile, a hexagon with a star polygon inside it. This one will tile without gaps, it is one of the Euclidean tilings. (3)
This is another common pattern in the Islamic geometric design vocabulary. There are an infinite number of patterns which can be created from this single line in a triangle. There are a limited number of integer divisions of the circle to start with, but the pattern line inside it can take almost any angle inside that triangle.
Can We Go Further?
Obviously. For this last example, I will take this method to a complex pattern that will be instantly recognizable. The method of reflecting a triangular division of a circle is exactly the same. Only the complexity of what we put in that triangular division of the circle changes.
We start with a one twenty-fourth division triangle. We make two decisions about the pattern lines with in that triangle. The end angle is also a one twenty-fourth angle. That pattern line does not continue across the triangle in a straight line. It is divided so that [A] and [B] are exacty equal lengths. We will get into how this is easily constructed later. This creates two more lines inside the triangle as shown. These obey strict rules, which we will also get into later. For now, let’s just look at whether this creates a pattern like the simple examples.
It obviously does or it wouldn’t be here. Reflection of the one twenty-fourth division 23 times to come around and meet itself creates a twelve sided tile, a dodecagon. When this is tiled edge to edge we get the figure above. Dodecagons tile with themselves to leave an equilateral triangle tile space open. This one is an Archimedean tiling. (3)
There are simple rules for filling these extra spaces in tilings for Islamic geometric pattern. The result below is the classic parallel sided 12 rosette in its closest hexagonal tiling.
We needed exactly one triangular division of the circle with one decision about how to break the pattern line inside it to define the creation of this pattern.
Question 3: Practically Speaking, How Does This Work?
Obviously nobody want to draw patterns by reflecting triangles 23 times. How will this be done in the forward direction, creating a simple layout?
Notes to the text:
(1) For very simple patterns, there is not much room for innovation. My layouts will look like everybody else’s layouts. For complex layouts, particularly with fivefold symmetry elements, I think that I have something interesting to say.
(2) See; Lewis F Day, Pattern Design, Dover Publications, Mineola, New York, 1999. Original 1933, 1903. Available free as a pdf from google books Here
(3) For most of the technical aspects of tiling which I will mention in these notes, a simple trip to wikipedia will give you good short definitions.